1/BigInteger的在C＃

我要讓1/BigInteger的在C＃

BigInteger.ModPow(1/BigInteger, 2,5);

但1/BigInteger總是返回0，這會導致，這個結果是0了。我試圖尋找一些c＃的BigDecimal類，但我什麼也沒找到。即使沒有BigDecimal，有什麼辦法可以計算出這個數字嗎？

來源

2013-01-06 Martin Ševic

'1/BigInteger'如何可能返回' 0'？。 'BigInters'默認值是'0'。它應該拋出'DivideByZeroException'。 –

從我對El Gamal的瞭解，我不認爲字面乘法逆是你正在尋找的。 – Rawling

@SonerGönül嗯，它不應該編譯，因爲它不會說'new BigInteger（）'，既不是'default（BigInteger）'。它應該抱怨在表達式中使用「類型」就像一個「變量」。 –

選擇的操作者/的過載，爲以下內容：

public static BigInteger operator /(
     BigInteger dividend, 
     BigInteger divisor 
)

參見BigInteger.Division Operator。如果結果在0和1之間（如果您的情況，dividend爲1時可能），因爲返回值是一個整數，所以返回0，如您所見。

你想用ModPow方法做什麼？你是否意識到2,5是兩個的論點，二，五，不是「兩點五」？你的意圖是「以平方5爲模數」嗎？

如果你想浮點除法，你可以使用：

1.0/(double)yourBigInt

注投給double。如果yourBigInt太大，這可能會失去精度，甚至「下溢」爲零。

來源

2013-01-06 11:36:54

1/a對於| a |> 1是0，因爲BigIntegers使用整數除法，其中忽略除法的小數部分。我不確定你對此期待什麼結果。

我假設你想要modular multiplicative inverse的a modulo m，而不是一個分數。如果a和m是共素，即gcd(a, m) = 1，則存在該逆。

鏈接的維基百科頁面列出了兩種標準算法計算模反元素：

Extended Euclidean algorithm，這適用於任意模
它速度快，但依賴輸入的運行時間。

我手邊沒有C＃代碼，但是從維基百科移植僞代碼應該是直截了當的。
使用歐拉定理：
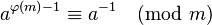
$i^{-1} = i^{φ(n)-1}$
這需要φ（M）的知識，即你需要知道m的首要因素。當m是素數時，它是一個受歡迎的選擇，因此當φ（m）= m-1時，它簡單地變爲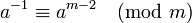 $a^{-1} = a^{p-2}$ 。如果你需要恆定的運行時間並且你知道φ（m），這是要走的路。

在C＃這成爲BigInteger.ModPow(a, phiOfM-1, m)

來源

2013-01-06 11:55:23 CodesInChaos

你可能是對的。請注意，'i'和'n'必須是相對主要的，因爲這是明確的。 –

例如，你需要得到d在下一：
3 * d = 1（MOD 9167368）

這同樣是：
3 * d = 1 + k * 9167368，其中k = 1,2,3，...

重寫它：
d =（1 + K * 9167368）/ 3

你的d必須與最低 k中的整數。
讓我們寫出下式：
d =（1 + K * FI）/ E

public static int MultiplicativeInverse(int e, int fi) 
     { 
      double result; 
      int k = 1; 
      while (true) 
      { 
       result = (1 + (k * fi))/(double) e; 
       if ((Math.Round(result, 5) % 1) == 0) //integer 
       { 
        return (int)result; 
       } 
       else 
       { 
        k++; 
       } 
      } 
     }

讓我們來測試此代碼：

Assert.AreEqual(Helper.MultiplicativeInverse(3, 9167368), 6111579); // passed

來源

2015-03-08 21:26:30

1/BigInteger的在C＃

回答

相關問題