Python與MATLAB計算積分到無限與不同的結果，替代（即擴大Gauss-Legendre積分到-x->無窮大）？

我得到了MATLAB的quadgk和Python的quad例程之間不一致的結果，用於（-x或0） - >無窮大的積分。我相信MATLAB版本是正確的（基於將參數flag從1切換到-1的感應檢查），而Python版本給出了錯誤的結果，在這種情況下爲0. MATLAB產生0.1022。 integrands是相同的，我已經把每一步的方法連起來，甚至將由MATLAB的quadgk生成的x值插入Python（這導致Python版本產生與MATLAB相同的值，只是將它們傳遞給integrand函數）。在這一點上，我正在尋找使用另一個例程，而不是SciPy，如Gauss-Legendre正交這裏https://sourceforge.net/projects/fastgausslegendrequadrature/，但我不知道如何將它從a/b範圍擴展到-a-> infinity（我見過這些方法只去一個有限的數量：Python與MATLAB計算積分到無限與不同的結果，替代（即擴大Gauss-Legendre積分到-x->無窮大）？

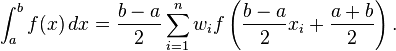$https://upload.wikimedia.org/math/a/7/f/$ Different intervals for Gauss-Legendre quadrature in numpy而b=np.Inf結果NaN還不能確定如何設置從返回的節點和權重的整合，雖然我一直在讀的轉型，但只有A和b有限範圍：https://pomax.github.io/bezierinfo/legendre-gauss.html要麼或者如果有人知道可以處理這個問題的Python庫 - 我不太喜歡quad雖然不是矢量化的，並且很可能會在Cython中編寫代碼，因爲我必須快速集成600,000個函數（即鏈接到th上面的C++庫鏈接）。這裏真奇怪的是，我設法得到了相同的結果，將vol輸入向上移動大於0.39，低於Python的結果在0處崩潰。非常混亂。任何幫助表示讚賞，它一直以來結石年......這裏是Python代碼：

from scipy.stats import norm, lognorm 
from scipy.integrate import quad 
import numpy as np 

def integrand(x, flag, F, K, vol, T2, T1): 
    d1 = (np.log(x/(x+K)) + 0.5 * (vol**2) * (T2-T1))/(vol * np.sqrt(T2 - T1)) 
    d2 = d1 - vol*np.sqrt(T2 - T1) 
    mu = np.log(F) - 0.5 *vol **2 * T1 
    sigma = vol * np.sqrt(T1) 
    value = lognorm.pdf(x, scale=np.exp(mu), s=sigma) * (flag * x*norm.cdf(flag * d1) - flag * (x+K)*norm.cdf(flag * d2)) 
    return value 

if __name__ == '__main__': 
     flag = 1 
     F = 54.31 
     K = 1.1967 
     vol = 0.1328 
     T2 = 0.0411 
     T1 = 0.0137 
     quad(integrand, 0, np.Inf, args=(flag, F, K, vol, T2, T1), epsabs=1e-12)[0]

這裏是MATLAB代碼（有保存integrand爲.M則可以在輸入腳本命令窗口）：

function value = integrand(x, flag, F,K,vol,T2,T1) 
d1 = (log(x ./ (x+K)) + 0.5 .* (vol.^2) .* (T2-T1)) ./ (vol .* sqrt(T2 - T1)); 
d2 = d1 - vol.*sqrt(T2 - T1); 
mu = log(F) - 0.5 .*vol .^2 .* T1; 
sigma = vol .* sqrt(T1); 
value = lognpdf(x, mu, sigma) .* (flag .* x.*normcdf(flag .* d1) - flag .* (x+K).*normcdf(flag .* d2)); 
end

％腳本部分

flag = 1 
F = 54.31 
K = 1.1967 
vol = 0.1328 
T2 = 0.0411 
T1 = 0.0137 
quadgk(@(x) integrand(x,flag, F, K, vol, T2, T1), 0, Inf, 'AbsTol',1e-12)

我要指出，MATLAB和Python使用四產生相同的結果時，這些輸入被傳遞，而不是（移位的ABO ve變量）：

current_opt = [ -1.0000 1.2075 0.1251 0.4300 0.0685 0.0411  
       1.0000 1.2075 0.0512 0.5600 0.0685 0.0411]

來源

2016-05-21 Matt

好吧，這很有趣。除非epsabs變量被設置的很高，否則整合會分崩離析。我已經設法使用epsabs=-1e1000在MATLAB和Python之間複製結果。儘可能慢，但至少可以工作。

來源

2016-05-21 18:34:57 Matt

Python與MATLAB計算積分到無限與不同的結果，替代（即擴大Gauss-Legendre積分到-x->無窮大）？

回答

相關問題