以下兩種方法中的哪一種使用正確的數學來旋轉點?如果是這樣,哪一個是正確的?適當的三角法旋轉原點的位置
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
float s = sin(angle);
float c = cos(angle);
// translate point back to origin:
p.x -= cx;
p.y -= cy;
// Which One Is Correct:
// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;
// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;
// translate point back:
p.x = xnew + cx;
p.y = ynew + cy;
}

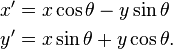
我不很明白。什麼是cx和cy?另外,你已經聲明瞭你的POINT類型的函數,但是它不返回一個POINT,或者其他任何東西。 – 2010-07-02 01:09:06
@Brian Hooper:+1用於指出有意義的變量名稱的好處;) – Cogwheel 2010-07-02 04:43:02